Veréis, el concepto de monomio es algo que hay que entender muy muy bien, ya que es base para la posterior ampliación al concepto de polinomio y es algo que os va a acompañar a lo largo de toda vuestra vida académica (siempre que deis matemáticas).
Los monomios son expresiones algebraicas que poseen dos partes fundamentales, una parte numérica o coeficiente y otra parte literal. Esto es,
de este modo, hemos de recordar siempre que la parte literal, cuyo adjetivo se debe precisamente a la palabra "letra", es aquella que contiene a la/s variable/s. En cambio, el coeficiente es, siempre, el numerillo que va multiplicando a la parte literal, que por conveniencia y lógica se coloca delante.
Cuando hago referencia a la lógica es por el propio sentido común, por el propio lenguaje algebraico en sí. Es decir, manejar monomios es como manejar objetos con las manos. De esta manera, si escribo $2·x^2$, lo normal es leer "dos por equis cuadrado" o "dos equis cuadrado", ahora bien, si escribo $x^2 ·2$, ¿cómo se leería?, pues "equis cuadrado por dos o equis cuadrado dos", lo cual es antinatural ¿no?, ¿no te resulta extraño?. Nadie habla invirtiendo el orden de los elementos del lenguaje, salvo el maestro jedi Yoda claro ;-p. Lo que hace que, por naturaleza, el coeficiente se coloque delante de la parte literal del monomio.
Vale, pues una vez aclarado esto, nos podemos hacer la siguiente pregunta...
¿Todos los monomios son distintos entre sí?... o ¿hay monomios semejantes?
Bueno, volvamos al sentido común... como dije antes, puesto que manejar monomios es como manejar objetos, vamos a plantearnos la siguiente situación:
Vamos a suponer que nos compramos un coche de la marca $x^3z$, extraña marca sí, pero muy buena. Y con el tiempo, nos toca una gran mega primitiva y no compramos un $x^3z^2$, mi pregunta es, ¿nos hemos comprado el mismo coche?, yo creo que no. De hecho, hasta al nombrarlos lo haríamos de diferente manera.
En cambio, si nos compramos un $x^3z$ y posteriormente otro $x^3z$, tendríamos en nuestra cochera dos $x^3z$, o lo que es lo mismo, $2x^3z$.
¿Qué diferencia ha habido entre este último ejemplo y el anterior?, pues que en el primer caso, no teníamos la misma parte literal y en el segundo sí. Y ahí es donde nos aparece el concepto de monomio semejante, y así podemos decir que:
"Dos monomio son semejantes si poseen la misma parte literal"
Fijaos que todo cobra sentido, además de manera muy muy natural. Por lo tanto, $3x^2$ y $5x^2$ sí son monomios semejantes. En cambio, $3x^2$ y $5x^4$, no.
Vale, ahora bien, las partes literales tienen un elemento que tambien caracteriza a nuestro monomio, y es...
Grado de un monomio
¿Qué es el grado de un monomio?, pues su definición es la siguiente:
"El grado de un monomio es el valor correspondiente a la suma de los exponentes de las variables que conforman su parte literal"
Esto que acabas de leer, puede parecer un galimatías, pero mejor lo vemos con un ejemplo (también lo puedes ver claro en el
videotutorial).
Supongamos que nos dan el monomio $-3x^5yz^2$ y nos piden que hallemos su grado. Bien, lo que tendremos que fijarnos es en los exponentes de cada una de las variables que conforman la parte literal. No olvidemos que en nuestro caso las variables son tres: $x,y$ y $z$. De esta manera, y teniendo en cuenta sus exponentes, tenemos que cada variable tiene los siguientes grados
$$x\rightarrow 5\\ y\rightarrow 1 \\ z\rightarrow 2$$
no olvides que si, sobre una variable no aparece ningún número, su exponente es $1$, ojo!!! es un error muy común poner $0$, y no!!!!, exponente que no aparezca, exponente $1$. SIEMPRE!!
Ok, visto lo visto, sumamos esos exponentes y tendríamos que $5+1+2=8$, con lo que el grado de nuestro monomio es $8$.
Ok, visto esto, vamos a ver cómo operar con los monomios.
Suma y resta de monomios
Para poder sumar y restar monomios, hay que tener presente una cosa...
"Sólo se podrán sumar y restar monomios que sean semejantes"
¿Por qué?... por lógica y por sentido común, acuérdate de los ejemplos vistos en el subapartado de monomios semejantes. De este modo, cuando queramos sumar o restar monomios semejantes, sumaremos o restaremos la parte numérica y la literal la dejaremos tal cual. Veámoslo con un ejemplo:
$$3x^2-7x^2=-4x^2\\2x^4+6x^4=8x^4$$
Fíjate que lo que hemos hecho es operar la parte numérica, pero sólo porque son semejantes. Si no fuesen semejantes... no podemos operar de esa manera. Por lo tanto, si nos plantan dos monomios no semejantes y nos piden que los sumemos, se quedarían como están esto es, $$3x^2+x^5=3x^2+x^5$$
y no podríamos hacer nada más.
Producto de monomios
Para esta operación sí podremos multiplicar cualquier tipo de monomios entre sí, sólo que, tanto en el producto como en el cociente o división, haremos uso de las propiedades de las potencias. Así que vamos a comenzar recordando estas, sobre todo las que usaremos:
- Para multilpicar dos potencias con la misma base, dejamos la base y sumamos los exponentes.
- Para dividir dos potencias con la misma base, dejamos la base y restamos los exponentes.
Así, para multiplicar dos monomios, multiplicamos los coeficientes y también, haciendo uso de la proiedad 1 comentada más arriba, las partes literales. Lo mejor... es verlo con un ejemplito:
$$2x^3·3x^4=(2·3)·x^{3+4}=6x^7$$
fíjate que he multiplicado los coeficientes y las partes literales. Y para operar las partes literales he usado la regla anteriomente comentada, es decir, he dejado la base y he sumado los exponentes, pues eran dos potencias con la misma base que se estaban multiplicando.
Pasemos ahora al cociente o división de dos monomios.
Cociente de monomios
Al igual que con en el producto de monomios, también podremos dividir cualquier tipo de monomios entre sí. Así que lo haremos de la siguiente manera: Para dividir dos monomios, dividiremos los coeficientes entre sí y las partes literales entre sí. Veámoslo con un ejemplo:
$$\frac{6x^7}{3x^2}=\frac{6}{3}·\frac{x^7}{x^2}=2·x^{7-2}=2x^5$$
fíjate cómo se ha operado. De forma muy parecida al caso de la operación pero, en esta ocasión, con un cociente o división.
Potencia de un monomio
En primer lugar, debemos pensar qué es la potencia de un monomio. Bueno, pues no es más que tomar un monomio y elevarlo a la potencia que sea. Por ejemplo: $\displaystyle (3x^2)^5$
Ahora bien, ¿cómo vamos a resolver este tipo de operaciones?, pues en primer lugar vamos a tener en cuenta un par de propiedades de las potencias que usaremos. Estas son las siguientes:
- $(a·b)^n=a^n·b^n$
- $(a^n)^m=a^{n·m}$
Es decir, cuando elevo un producto a una potencia, es elevar cada factor a la potencia. Y cuando una potencia está elevada a otra, permanece la parte literal y se multiplican los exponentes. Pero, como siempre, lo mejor es verlo con un ejemplo:
$$(3x^2)^3=3^3·(x^2)^3=27·x^6=27x^6$$
. ¿Por qué esa "q" mayúscula?, bueno, la razón es por la palabra "quotient" (inglés) o "quoziente" (italiano), cociente. Y es que todos esos números son fracciones, es decir, por ejemplo, 
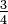, también se puede escribir 3/4. Es decir:
= 
. Y este conjunto está formado por todos aquellos números que no pueden expresarse como un número racional. O lo que es lo mismo, y hablando en plata, son todos aquellos números decimales que tienen infinitos decimales y los cuales no siguen un patrón de repetición determinado. Por ejemplo, 
