¿Cuáles son los conjuntos numéricos?... Reales, naturales, enteros, racionales.
Buenas!!!! vamos a estrenar el blog con una entrada en la que explicaré cómo funcionan, en matemáticas, los conjuntos numéricos.
Téngase en cuenta que esta explicación está desarrollada conforme al nivel de exigencia de un primer curso de la educación secundaria. Con lo que no entraré en detalles científicos rigurosos tales como axiomáticas, etc...
Bien, en matemáticas tenemos varios tipos de conjuntos numéricos. Por un lado tenemos los números naturales, que se denota por ℕ. Este conjunto, amén de la axiomática de Peano que lo define perfectamente, se construye por necesidad. Me explico, hace miles de años, el hombre y la mujer sienten la necesidad de contar. Por ejemplo, necesitaban saber cuántos hijos tenían, o cuántos corderos poseían en su rebaño. De este modo, surgieron los números 1, 2, 3, 4, ... Con lo que
ℕ={1,2,3,...}
Por otro lado, conforme fue aumentando la necesidad de contar o de llevar una determinada contabilidad, surgió la consideración de los números negativos. Hay que tener en cuenta que estos nacen con las operaciones suma y diferencia, de hecho, en el renacimiento se advierte de su existencia, aunque ya se utilizaban en la India. Añadido a ellos, también se considera al cero (0), que también era usado por matemáticos hindúes desde hacía siglos. Este conjunto de números enteros se denota por ℤ, ¿y por qué con una z?, pues porque la palabra números, en alemán, se escribe zahlen. De este modo se convino a utilizar esa notación.
Ok, de este modo... ℤ={...,-3,-2,-1,0,1,2,3,...}.
Ahora bien, ¿están los números naturales contenidos en los enteros?. Pues sí, de hecho, los naturales son realmente todos los números enteros estrictamente mayores que cero. De esta manera, ℕ⊆ℤ.
Por último, tenemos los números racionales, que se denotan por  . ¿Por qué esa "q" mayúscula?, bueno, la razón es por la palabra "quotient" (inglés) o "quoziente" (italiano), cociente. Y es que todos esos números son fracciones, es decir, por ejemplo,
. ¿Por qué esa "q" mayúscula?, bueno, la razón es por la palabra "quotient" (inglés) o "quoziente" (italiano), cociente. Y es que todos esos números son fracciones, es decir, por ejemplo, 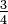 , también se puede escribir 3/4. Es decir:
, también se puede escribir 3/4. Es decir:
 . ¿Por qué esa "q" mayúscula?, bueno, la razón es por la palabra "quotient" (inglés) o "quoziente" (italiano), cociente. Y es que todos esos números son fracciones, es decir, por ejemplo,
. ¿Por qué esa "q" mayúscula?, bueno, la razón es por la palabra "quotient" (inglés) o "quoziente" (italiano), cociente. Y es que todos esos números son fracciones, es decir, por ejemplo, 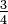 , también se puede escribir 3/4. Es decir:
, también se puede escribir 3/4. Es decir: = {....- ¾, - ½, - ¼ , 0, ¼ , ½, ¾,.....}
= {....- ¾, - ½, - ¼ , 0, ¼ , ½, ¾,.....}
Un momento... ¿qué ocurre si consideramos -6/3?, recordemos que -6:3=-2, con lo que tendríamos un número entero. De este modo, ℕ⊆ℤ⊆ .
.
 .
.
Finalmente, a parte de estos números racionales, enteros, naturales y demás, tenemos también los irracionales, los cuales se denotan por  . Y este conjunto está formado por todos aquellos números que no pueden expresarse como un número racional. O lo que es lo mismo, y hablando en plata, son todos aquellos números decimales que tienen infinitos decimales y los cuales no siguen un patrón de repetición determinado. Por ejemplo, √2.
. Y este conjunto está formado por todos aquellos números que no pueden expresarse como un número racional. O lo que es lo mismo, y hablando en plata, son todos aquellos números decimales que tienen infinitos decimales y los cuales no siguen un patrón de repetición determinado. Por ejemplo, √2.
 . Y este conjunto está formado por todos aquellos números que no pueden expresarse como un número racional. O lo que es lo mismo, y hablando en plata, son todos aquellos números decimales que tienen infinitos decimales y los cuales no siguen un patrón de repetición determinado. Por ejemplo, √2.
. Y este conjunto está formado por todos aquellos números que no pueden expresarse como un número racional. O lo que es lo mismo, y hablando en plata, son todos aquellos números decimales que tienen infinitos decimales y los cuales no siguen un patrón de repetición determinado. Por ejemplo, √2.
Bueno, una vez visto esto, podemos concluir diciendo que entre os números racionales y los números irracionales tendríamos todos los números necesarios para la vida cotidiana, para la vida real. Es por ello que de la unión de esos dos conjuntos surgen los números reales. Por tanto,

para ilustrar con más detalle y de una forma más amena todo lo expuesto,

(Imágenes: www.portaleducativo.net)
No hay comentarios:
Publicar un comentario